第9講 Laurent展開と留数定理
Laurent展開
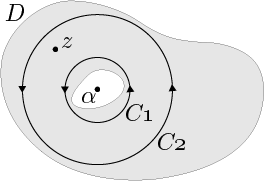
$\alpha\in\mathbf{C}$,$0 < R_1 < R_2$ とする.一価複素関数 $f$ が
$\{\,z\ |\ R_1\le |z-\alpha| \le R_2\,\}$ を含む領域で正則ならば,$f$ はその内部 $\{\,z\ |\ R_1< |z-\alpha| < R_2\,\}$ において
$\displaystyle f(z)=\sum_{n=-\infty}^\infty a_n(z-\alpha)^n$
$\displaystyle a_n=\dfrac{1}{2\pi i}\oint_{|w-\alpha|=r}\dfrac{f(w)}{(w-\alpha)^{n+1}}dw$
と表わすことができる.ここで,$r$ は $R_1\le r\le R_2$ なる任意の実数である
証明.
負の冪で表される $\displaystyle \sum_{n=-\infty}^{-1} a_n(z-\alpha)^n$
の部分はこの展開の
主要部と呼ばれる.
$\alpha$ は必ずしも特異点である必要はないが,Laurent展開は特異点を中心に行われることが多い.
$\alpha$ が特異点であるとき
$f(z)=\dfrac{a_{-m}}{(z-\alpha)^m}+\dfrac{a_{-m+1}}{(z-\alpha)^{m-1}}+$$\cdots+a_0+a_1(z-\alpha)+\cdots$
と,主要部が $m$ 個の項からなるならば,$\alpha$ は $m$ 位の
極であるという.
主要部が無限個の項となるならば $\alpha$ は
真性特異点であるという.
$\alpha$ が特異点であっても,Laurent展開が
$f(z)=a_0+a_1(z-\alpha)+\cdots$
と,主要部をもたない場合もあり,その場合は $f(\alpha)=a_0$ と新たに定義することにより特異性を解消できるので,$\alpha$ は
除去可能な特異点と呼ばれる.
この他,$\log{z}$ などの多価関数の分岐点も特異点である.
多価関数のLaurent展開は冪級数展開と同様に,分枝ごとに考えればできないことはないのだが,係数が周回積分で表されるため,分岐点のまわりでの展開になるとさらにきつめの条件を課さなければならなくなり,あまり有用とも言えないのでここでは多価関数は念頭にはおかないことにする.
Laurent展開の実際の計算,収束域の判定は既知の冪級数展開等を用いて行われることが多い.
$\dfrac{e^z}{z^3}$ を $z=0$ のまわりで展開すると
$\dfrac{e^z}{z^3}
=\dfrac{1}{z^3}\Big(1+z+\dfrac{z^2}{2!}+\dfrac{z^3}{3!}+\dfrac{z^4}{4!}+\dfrac{z^5}{5!}+\cdots\Big)\\[1mm]
\hspace{15pt}=\dfrac{1}{z^3}+\dfrac{1}{z^2}+\dfrac{1}{2!z}+\dfrac{1}{3!}+\dfrac{z}{4!}+\dfrac{z^2}{5!}+\cdots$
となり,収束域は $\mathbf{C}\backslash\{\,0\,\}$,$z=0$ は $3$ 位の極である.
$\dfrac{1}{z(z+1)}$ を $z=0$ のまわりで展開すると
$\dfrac{1}{z(z+1)}
=\dfrac{1}{z}(1-z+z^2-z^3+\cdots)\\[1mm]
\hspace{39pt}=\dfrac{1}{z}-1+z-z^2+\cdots$
となり,収束域は $|z| < 1 $,$z\neq 0$ より $\{\,z\ |\ 0 < |z| < 1\,\}$,$z=0$
は $1$ 位の極である.
同じく $\dfrac{1}{z(z+1)}$ を $z=-1$ のまわりで展開すると
$\dfrac{1}{z(z+1)}
=\dfrac{1}{z+1}\cdot\dfrac{-1}{1-(z+1)}\\[1mm]
\hspace{39pt}=-\dfrac{1}{z+1}\{1+(z+1)+(z+1)^2+\cdots\}\\[1mm]
\hspace{39pt}=-\dfrac{1}{z+1}-1-(z+1)-\cdots$
となり,収束域は $|z+1| < 1 $,$z\neq -1$ より $\{\,z\ |\ 0 < |z+1| < 1\,\}$,$z=-1$ は $1$ 位の極である.
$\dfrac{\sin{z}}{z}$ を $z=0$ のまわりで展開すると
$\dfrac{\sin{z}}{z}
=\dfrac{1}{z}\Big(z-\dfrac{z^3}{3!}+\dfrac{z^5}{5!}+\cdots\Big)\\[1mm]
\hspace{23pt}=1-\dfrac{z^2}{3!}+\dfrac{z^4}{5!}+\cdots$
となるので,$z=0$ は除去可能な特異点である.$\dfrac{\sin{z}}{z}\bigg|_{z=0}=1$ と新たに定義することにより収束域は $\mathbf{C}$ 全体とすることができる.
$e^{1/z}$ を $z=0$ のまわりで展開すると
$e^{1/z}
=1+\dfrac{1}{z}+\dfrac{1}{2!z^2}+\dfrac{1}{3!z^3}+\cdots$
となり,収束域は $\mathbf{C}\backslash\{\,0\,\}$,$z=0$ は真性特異点である.
$z=\alpha$ が $f$ の $m$ 位の極であるための必要十分条件は
$\displaystyle \lim_{z\to \alpha}(z-\alpha)^mf(z)$ が $0$ 以外の有限の値となることである(極の定義から明らかであろう).このことを用いて,Laurent展開を実行しなくても,ある程度の予想のもとに特異点の種類が判定できることも多い.
$f(z)=\dfrac{1}{z^3(z-3i)^4}$ の特異点は$z=0,3i$ であり
$\displaystyle \lim_{z\to0}z^3f(z)=\lim_{z\to 0}\dfrac{1}{(z-3i)^4}=\dfrac{1}{81}(\neq0)$
より,$z=0$は3位の極.また
$\displaystyle \lim_{z\to3i}(z-3i)^4f(z)=\lim_{z\to 3i}\dfrac{1}{z^3}=\dfrac{i}{27}(\neq0)$
より,$z=3i$は4位の極とわかる.
$g(z)=\dfrac{1}{z\sin{z}}$ の特異点は $z\sin{z}=0$ となる点なので $z=n\pi i\ (n\in\mathbf{Z})$ であるが,
$\sin{z}=z-\dfrac{z^3}{3!}+\cdots$ から,$z=0$ は $2$ 位の極,他は $1$位の極であろうと予想できる.実際
$\displaystyle \lim_{z\to 0}z^2g(z)
=\lim_{z\to0}\dfrac{z}{\sin{z}}=1(\neq0)$
より,$z=0$は $2$ 位の極,$n\neq0$のとき
$\displaystyle \lim_{z\to n\pi i}(z-n\pi i)h(z)\\[1mm]
\hspace{30pt}=\lim_{z\to n\pi i}\dfrac{z-n\pi i}{z\sin{z}}\\[1mm]
\hspace{30pt}=\lim_{z\to 0}\dfrac{z}{(z+n\pi i)\sin(z+n\pi i)}\\[1mm]
\hspace{30pt}=\lim_{z\to 0}\dfrac{z}{(z+n\pi i)(-1)^n\sin{z}}\\[1mm]
\hspace{30pt}=\dfrac{1}{(-1)^nn\pi}(\neq0)$
より,$z=n\pi i\ (n\in\mathbf{Z}\backslash\{0\})$ は $1$ 位の極であるとわかる.
留数定理
複素関数 $f$ をその特異点 $\alpha$ のまわりに
$\displaystyle f(z)=\sum_{n=-\infty}^\infty a_n(z-\alpha)^n$
とLaurent展開したときの $-1$ 次の項の係数 $a_{-1}$ を $f$ の $\alpha$ における
留数と呼び
$\underset{z=\alpha}{\mathrm{Res}}f(z)$
と表わす.
$a_{-1}$に特に着目する理由は,前節で述べたように,Laurent展開の各係数は
$\displaystyle a_n=\dfrac{1}{2\pi i}\oint_{|z-\alpha|=r}\dfrac{f(w)}{(w-\alpha)^{n+1}}dw$
と表され,特に
$\displaystyle a_{-1}=\dfrac{1}{2\pi i}\oint_{|z-\alpha|=r}f(w)dw$
と,$a_{-1}$ が $f$ の周回積分を与えているからである.
$z^n\ (n\in\mathbf{Z})$ の周回積分が
$\displaystyle \oint_{|z|=r}z^ndz=\left\{\begin{array}{ll}2\pi i&\mbox{if $n=-1$}\\0&\mbox{if $n\neq -1$}\end{array}\right.$
であったことを思い出そう.このことから
$\displaystyle f(z)=\sum_{n=-\infty}^\infty a_n(z-\alpha)^n$
の両辺を積分すると(項別積分が許されるとして),右辺は $-1$ 乗の項だけ残り
$\displaystyle \oint_{|z-\alpha|=r}f(z)dz=\sum_{n=-\infty}^\infty a_n\oint_{|z-\alpha|=r}(z-\alpha)^ndz =a_{-1}2\pi i$
となる.もちろんこれは形式的な計算ではあるが「$-1$ 乗だけが特別」であることが周回積分の計算において極めて重要な意味をもつことは意識しておきたい.
そこで,与えられた関数の留数をどのように計算するかが問題になるが,$\alpha$ が $m$位の極である場合は
$\displaystyle \underset{z=\alpha}{\mathrm{Res}}f(z)=\lim_{z\to\alpha}\dfrac{1}{(m-1)!}\dfrac{d^{m-1}}{dz^{m-1}}(z-\alpha)^mf(z)$
と計算することができる
詳しく!.
$\alpha$ が $m$ 位の極ならば
$f(z)=\dfrac{a_{-m}}{(z-\alpha)^m}+\cdots+\dfrac{a_{-1}}{z-\alpha}+a_0+\cdots$
と表わされるのであるから
$(z-\alpha)^mf(z)=a_{-m}+\cdots+a_{-1}(z-\alpha)^{m-1}+a_0(z-\alpha)^m+\cdots$
従って
$\dfrac{d^{m-1}}{dz^{m-1}}(z-\alpha)^mf(z)=(m-1)!a_{-1}+m!a_0(z-\alpha)+\cdots$
となる.
$\dfrac{e^{2z}}{z^3}$ において,$z=0$ は $3$ 位の極であるから
$\displaystyle \underset{z=0}{\mathrm{Res}}\dfrac{e^{2z}}{z^3}
=\lim_{z\to 0}\dfrac{1}{2!}\dfrac{d^2}{dz^2}e^{2z}=\lim_{z\to0}2e^{2z}=2$
$\dfrac{1}{\sin{z}}$ において,$z=n\pi\ (n\in\mathbf{Z})$ は $1$ 位の極であるから
$\displaystyle \underset{z=n\pi}{\mathrm{Res}}\dfrac{1}{\sin{z}}
=\lim_{z\to n\pi}\dfrac{(z-n\pi)}{\sin{z}}=\lim_{z\to 0}\dfrac{z}{\sin(z+n\pi)}=(-1)^n$
$e^{1/z}$ において,$z=0$ は真性特異点であるから,Laurent展開を実行して
$e^{1/z}=1+\dfrac{1}{z}+\dfrac{1}{2!z^2}+\cdots$
より $\displaystyle \underset{z=0}{\mathrm{Res}}\ e^{1/z}=1$.
複素関数 $f$ が領域 $D$ において有限個の特異点をもつとき,$D$ に含まれる任意の閉曲線 $C$ に沿った周回積分は
$\displaystyle \oint_Cf(z)dz=2\pi i\sum_{j=1}^N\underset{z=c_j}{\mathrm{Res}}f(z)$
と,$C$の内部に含まれる特異点 $c_1,c_2,\ldots,c_N$ における留数の和(の $2\pi i$ 倍)で与えられると主張するのが
留数定理である
証明.
$\dfrac{e^{2z}}{z^3}$ において,$z=0$ は $3$ 位の極で
$\displaystyle \underset{z=0}{\mathrm{Res}}\dfrac{e^{2z}}{z^3}=2$ だったから
$\displaystyle \oint_{|z|=1}\dfrac{e^{2z}}{z^3}dz
=2\pi i\cdot\underset{z=0}{\mathrm{Res}}\dfrac{e^{2z}}{z^3}
=4\pi i$
となる.この形の積分は前講で見た一般型のCauchyの積分公式によっても計算できる.
留数定理はCauchyの積分公式をさらに拡張したものと言ってもよい.
$\dfrac{1}{\sin{z}}$ において,$z=n\pi\ (n\in\mathbf{Z})$ は $1$ 位の極で
$\displaystyle \underset{z=n\pi}{\mathrm{Res}}\dfrac{1}{\sin{z}}=(-1)^n$ であった.例えば円周 $\{\,z\ |\ |z-1|=3\,\}$ の内部に含まれる特異点は $0$ と $\pi$ であるから
$\displaystyle \oint_{|z-1|=3}\dfrac{dz}{\sin{z}}
=2\pi i\Big\{\underset{z=0}{\mathrm{Res}}\dfrac{1}{\sin{z}}+\underset{z=\pi}{\mathrm{Res}}\dfrac{1}{\sin{z}}\Big\}\\[1mm]
\hspace{56pt}=2\pi i\{1+(-1)\}=0
$
となる.
$e^{1/z}$ において,$z=0$ は真性特異点で $\displaystyle \underset{z=0}{\mathrm{Res}}\ e^{1/z}=1$ だったから
$\displaystyle \oint_{|z|=1}e^{1/z}dz
=2\pi i\cdot\underset{z=0}{\mathrm{Res}}\ e^{1/z}=2\pi i
$
となる.
 負の冪で表される $\displaystyle \sum_{n=-\infty}^{-1} a_n(z-\alpha)^n$
の部分はこの展開の主要部と呼ばれる.
負の冪で表される $\displaystyle \sum_{n=-\infty}^{-1} a_n(z-\alpha)^n$
の部分はこの展開の主要部と呼ばれる.