第8講 冪級数とTaylor展開
冪級数
$\alpha,\ a_n\ (n=0,1,2,\ldots)$ を複素数の定数として
収束半径の判定には次が有用である定理8.1pdf:
$\displaystyle \sum_{n=0}^\infty a_n(z-\alpha)^n$
という形で表される複素関数を $\alpha$ を中心とする冪級数という.
これは無限和なので,$z$ がどのような範囲の数であれば収束のかがまず問題になる.
そこで
$|z-\alpha| < \rho$ ならば級数は収束する
$|z-\alpha| > \rho$ ならば級数は発散する
ような $\rho$ のことをその級数の収束半径と呼び,
開円板 $\{\,z\ |\ |z-\alpha| < \rho\,\}$ のことを収束域(収束円)と呼ぶ.
収束半径 $\rho$ は正の実数であるが,すべての $z\in\mathbf{C}$ に対して級数が収束するときは $\rho=\infty$「収束半径は無限大」という言い方をする.その場合の収束域は $\mathbf{C}$ 全体ということになる.
また,$z=\alpha$ のときしか級数が収束しない場合は$\rho=0$,その場合の収束域は $\{\,\alpha\,\}$ である.
$|z-\alpha| > \rho$ ならば級数は発散する
$\displaystyle \rho=\lim_{n\to\infty}\left|\dfrac{a_n}{a_{n+1}}\right|$
この右辺の極限が( $\infty$ の場合も含めて)存在すればよいが,そうでない場合は次の判定法が用いられる定理8.2pdf:
$\displaystyle \rho=\dfrac{1}{\limsup_{n\to\infty}\sqrt[n]{|a_n|}}$
特異点
複素関数の特異点とは,その点で関数の値が定義されていないか,定義されていても微分可能でないような点のことをいう.
典型的な特異点は,分母が $0$ になるような点や,多価関数の分岐点などである.
Taylor展開
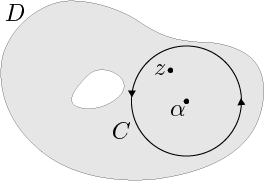
ある領域 $D$ で正則な関数 $f$ は $D$ において冪級数展開できる.
すなわち,各 $\alpha\in D$ に対して $D_r=\{\,z\ |\ |z-\alpha| < r\,\}\subset D$ となるように $r>0$ をとれば
 基本的な冪級数展開として,いわゆる「無限等比級数」
基本的な冪級数展開として,いわゆる「無限等比級数」
また,指数関数・三角関数・双曲線関数についてのおなじみの展開式もやはり複素関数として成り立つ:
$\displaystyle f(z)=\sum_{n=0}^\infty \dfrac{1}{2\pi i}\oint_{|w-\alpha|=r}\dfrac{f(w)}{(w-\alpha)^{n+1}}dw\cdot (z-\alpha)^n,\\\hspace{170pt}\quad z\in D_r$
と表わすことができる証明pdf.

$\dfrac{1}{1-z}=1+z+z^2+z^3+\cdots$
は複素関数としても成り立つ.この級数の収束域が単位開円板 $\{\,z\ |\ |z| < 1\,\}$ であることは容易にわかる.
$\dfrac{1}{1-z}$ の特異点は $z=1$ であり,展開の中心 $z=0$ からこの特異点までの距離が収束半径となっていることに注目しよう.また,指数関数・三角関数・双曲線関数についてのおなじみの展開式もやはり複素関数として成り立つ:
$e^z=1+z+\dfrac{z^2}{2!}+\dfrac{z^3}{3!}+\cdots$
$\cos{z}=1-\dfrac{z^2}{2!}+\dfrac{z^4}{4!}-\cdots$
$\sin{z}=z-\dfrac{z^3}{3!}+\dfrac{z^5}{5!}-\cdots$
$\cosh{z}=1+\dfrac{z^2}{2!}+\dfrac{z^4}{4!}+\cdots$
$\sinh{z}=z+\dfrac{z^3}{3!}+\dfrac{z^5}{5!}+\cdots$
これらの収束域が $\mathbf{C}$ 全体であることも容易に確認できよう.
$\cos{z}=1-\dfrac{z^2}{2!}+\dfrac{z^4}{4!}-\cdots$
$\sin{z}=z-\dfrac{z^3}{3!}+\dfrac{z^5}{5!}-\cdots$
$\cosh{z}=1+\dfrac{z^2}{2!}+\dfrac{z^4}{4!}+\cdots$
$\sinh{z}=z+\dfrac{z^3}{3!}+\dfrac{z^5}{5!}+\cdots$
Cauchyの積分公式の拡張
複素関数 $f$ が領域 $D$ で正則ならば,$f$ は $D$ の各点で任意回微分可能で,その $n\ (\in\mathbf{N})$ 階微分係数は
$\displaystyle f^{(n)}(\alpha)=\dfrac{n!}{2\pi i}\oint_{|w-\alpha|=r}\dfrac{f(w)}{(w-\alpha)^{n+1}}dw,\quad \alpha\in D$
により与えられる証明pdf.
このことは,冪級数が項別微分可能なことから
$\displaystyle f(z)=\sum_{n=0}^\infty \dfrac{f^{(n)}(\alpha)}{n!}(z-\alpha)^n$
という形になっているはずで,これと前節で見た展開係数を比べるとわかる.
また,上式はCauchyの積分公式
$\displaystyle f(\alpha)=\dfrac{1}{2\pi i}\oint_{|w-\alpha|=r}\dfrac{f(w)}{w-\alpha}dw$
を形式的に積分記号下で $\alpha$ について微分した形になっていることにも注目しよう.