曲線
$\mathbf{C}$ における
曲線とは,$\mathbf{R}$ の閉区間で定義され $C$ に値をとる(有限個の点を除き)微分可能な関数,あるいはその像集合
$\{\,z(t)\ |\ t_1\le t \le t_2\,\}$ $(t_1,t_2\in\mathbf{R},\ t_1 < t_2)$
のことをいう.曲線の向きは原則として上のように表したときのパラメータ $t$ が増加する向きを正の向きと定める.
曲線 $C$ の向きを逆にしたものを考えるときは $-C$ と表す.
$z=0$ から $z=1+i$ へ至る曲線としては
$C_1=\{\,t+it\ |\ 0\le t\le 1\,\}$
のような線分や
$C_2=\{\,t+it^2\ |\ 0\le t\le 1\,\}$
のような放物線の一部などが考えられる.
あるいは
$C_3=\{\,t\ |\ 0\le t\le 1\,\}\cup\{\,1+it\ |\ 0\le t\le 1\,\}$
のように $0\rightarrow 1\rightarrow 1+i$ と
途中で折れ曲がっているものでもよい.
また,「逆向きにしたもの」とは $z=1+i$ から $z=0$ へ至る曲線で,例えば上の $C_1$ であれば
$-C_1=\{\,(1-t)+i(1-t)\ |\ 0\le t\le 1\,\}$
と表わすことができる.
ここに挙げた以外にも無数の曲線を考えることができるが,
曲線の性質そのものがここでの興味の対象ではないので,さらに条件が必要な場合はその場面に応じて設定することにする.
複素積分
複素関数 $f(z)$ の曲線 $C=\{\,z(t)\,|\,t_1\le t\le t_2\,\}$ に沿った積分を
$\displaystyle \int_Cf(z)\,dz=\int_{t_1}^{t_2}f(z(t))\,z'(t)\,dt$
により定義する.
$f(x+yi)=u(x,y)+v(x,y)i$ ,$z(t)=x(t)+y(t)i$ と表すとき,$z'(t)=x'(t)+y'(t)i$ であり
$\displaystyle \int_C f(z)dz
=\displaystyle \int_{t_1}^{t_2}\{\,u(x(t),y(t))+iv(x(t),y(t))\,\}\\
\hspace{120pt}\times\{\,x'(t)+iy'(t)\,\}\,dt\\[1mm]
\hspace{40pt}=\ \cdots\\[1mm]
\hspace{40pt}=\displaystyle \int_{\tilde{C}}u(x,y)dx-v(x,y)dy\\
\hspace{95pt}\displaystyle +i\int_{\tilde{C}}v(x,y)dx+u(x,y)dy$
となる.ここで,$\tilde{C}=\{\,(x(t),y(t))\,|\,t_1\le t\le t_2\,\}$ である.
このように,複素積分の実際の計算は実関数の線積分の計算に帰着される.
従って,線型性などの基本的な性質は実関数の場合と同様に成り立つし,
積分路のとり方によって積分の値が異なり得るということもやはり同様である.
前項で挙げた $z=0$ から $z=1+i$ へ至る三つの曲線
$C_1=\{\,t+it\ |\ 0\le t\le 1\,\}$
$C_2=\{\,t+it^2\ |\ 0\le t\le 1\,\}$
$C_3=\{\,t\ |\ 0\le t\le 1\,\}\cup\{\,1+it\ |\ 0\le t\le 1\,\}$
に沿って積分 $\displaystyle \oint_{C_j}\bar{z}\,dz$ $(j=1,2,3)$ を考える.
$C_1$ 上では $z=t+it$,$dz=(1+i)dt$ だから
$\displaystyle \int_{C_2}\bar{z}dz
=\int_0^1\overline{(t+it)}(1+i)\,dt\\[1mm]
\hspace{30pt}\displaystyle =\int_0^1(t-it)(1+i)\,dt\\[1mm]
\hspace{30pt}\displaystyle =\int_0^12t\,dt=1$
$C_2$ 上では $z=t+it^2$,$dz=(1+2it)dt$ だから
$\displaystyle \int_{C_3}\bar{z}dz=\int_0^1\overline{(t+it^2)}(1+2it)dt\\[1mm]
\hspace{30pt}\displaystyle =\int_0^1(t-it^2)(1+2it)dt\\[1mm]
\hspace{30pt}\displaystyle =\int_0^1(t+it^2+2t^3)dt=1+\dfrac{i}{3}$
$C_3$ の
$\{\,t\,|\,0\le t\le 1\,\}$ 上では $z=t,\ dz=dt$,
$\{\,1+i\,t\,|\,0\le t\le 1\,\}$ 上では $z=1+it,\ dz=idt$ だから
$\displaystyle \int_{C_1}\bar{z}\,dz
=\int_0^1\bar{t}\,dt+\int_0^1\overline{1+it}\,idt\\[1mm]
\hspace{30pt}\displaystyle =\int_0^1t\,dt+\int_0^1(1-it)\,idt\\[1mm]
\hspace{30pt}\displaystyle =\dfrac{1}{2}+\Big(1-\dfrac{1}{2}i\Big)i=1+i$
微分と積分
当然というべきであろうか,次が成り立つ:
複素関数 $f$ が
原始関数をもつとき,
すなわち,ある領域 $D$ で正則な関数 $F$ によって
$f(z)=F'(z)\quad(z\in D)$ と表されるとき,$D$ 内で点 $a$ から点 $b$ に到る任意の曲線 $C$ に対して
$\displaystyle \int_Cf(z)dz=F(b)-F(a)$
が成り立つ
証明pdf.
この場合,積分の値は経路によらずに定まるので,$\displaystyle \int_a^bf(z)dz$ という表記が可能になり,一変数の実定積分と同様に計算される.
$\dfrac{d}{dz}e^z=e^z\quad(\forall z\in\mathbf{C})$
だったから
$\displaystyle \int_{-\pi i}^{\pi i/2 }e^z\,dz=e^z\,\Big|_{-\pi i}^{\pi i/2 }=e^{\pi i/2}-e^{-\pi i}=1+i$
周回積分
始点と終点が一致するような曲線を
閉曲線というが,
閉曲線 $C$ に沿う複素積分を複素周回積分と呼び
$\displaystyle \oint_Cf(z)\,dz$
のように表す.
この場合の積分路の向きは $C$ がその内部($C$ によって囲まれる有界領域)を左手に見て進む向きとする.
特に,$z^n\ (n\in\mathbf{Z})$ の,円周 $C_r=\{\,z\ |\ |z|=r\,\}\ (r>0)$ に沿った周回積分は
$\displaystyle \oint_{C_r}z^n\,dz
=\left\{\begin{array}{ll}
2\pi i&(n=-1)\\
0&(n\neq -1)
\end{array}\right.
$
となる
詳しく!.
始点・終点を
$z=r$ にとると $C_r=\{\,re^{i\theta}\,|\,0\le \theta \le 2\pi\,\}$
と表せるから,$z=re^{i\theta}$,$dz=ire^{i\theta}d\theta$ より
$\displaystyle \oint_Cz^n\,dz
=\int_0^{2\pi}r^ne^{in\theta}ire^{i\theta}d\theta\\[1mm]
\hspace{30pt}=\displaystyle i\int_0^{2\pi}r^{n+1}e^{i(n+1)\theta}d\theta\\[1mm]
\hspace{30pt}=\left\{\begin{array}{l}
\displaystyle i\int_0^{2\pi}d\theta=2\pi i\quad(n=-1)\\[3mm]
\dfrac{r^{n+1}}{n+1}e^{i(n+1)\theta}\Big|_0^{2\pi}
=0\quad(n\neq -1)
\end{array}\right.
$
始点・終点を他の点にとっても同じ結果が得られることは容易に確かめられる.
この $\dfrac{1}{z}$ だけが特別であって他はすべて $0$ という結果は,複素積分の計算全般において非常に重要な事実である.
例えば $z^2$ については $\dfrac{z^3}{3}$ という原始関数が存在するので,前項で見た計算と同様に,任意の閉曲線 $C$ について(始点・終点を $z=a$ とすると)
$\displaystyle \oint_Cz^2dz=\dfrac{z^3}{3}\,\bigg|_a^a=\dfrac{a^3}{3}-\dfrac{a^3}{3}=0$
ということが成り立つのは当然と言える.
$\dfrac{1}{z^2}$ にしても原始関数 $-\dfrac{1}{z}$ が存在するので,周回積分の値は(閉曲線が特異点 $z=0$ を通らない限り)やはり $0$ になる.
では,$\dfrac{1}{z}$ の原始関数は存在しないのかと言うと,
実は存在して,それが複素対数関数 $\log{z}$ なのである.
にも拘らず周回積分の値が $0$ にならないのは,複素対数関数が多価関数であって通常の関数とは扱いが異なるという事情がある.そういう理由があって第3講の初等関数(1)では対数関数に触れなかったのだが,他の多価関数も含めこれについては講を改めて述べることにする.
Cauchyの積分定理
次のCauchyの積分定理は,複素関数論における基本定理である:
複素関数 $f$ が
単連結領域 $D$ で正則ならば,$D$ に含まれる任意の閉曲線 $C$ について
$\displaystyle \oint_Cf(z)dz=0$
が成り立つ
略証pdf.
ここで,単連結領域とは「穴のない」領域のことをいう
例えば?.
例えば全平面$\mathbf{C}$や開円板,半平面などは単連結だが,$\mathbf{C}\backslash\{0\}$や$\{\,z\ |\ 1 < |z| < 2\,\}$などの領域は単連結ではない.
この「単連結」という条件は重要である.前項で見た
$\dfrac{1}{z}$ は $\mathbf{C}\backslash\{0\}$ で正則であるが,この定義域は単連結ではない「穴の開いた」領域であり,
円周$\{\,z\ |\ |z|=r\,\}$は「単連結領域に含まれる閉曲線」でないためにCauchyの積分定理の条件を満たしていなかったのである.
指数関数 $e^z$ は $\mathbf{C}$ 全体で正則であり,$\mathbf{C}$ はもちろん単連結領域であるから,$\mathbf{C}$ の任意の閉曲線 $C$ に対して
$\displaystyle \oint_Ce^zdz=0$
が成り立つ.このことは $e^z$ が $\mathbf{C}$ 全体で定義された原始関数をもつことからも明らかである.
一方,$\dfrac{1}{z}$ については
$\displaystyle \oint_{|z|=r}\dfrac{1}{z}\,dz=2\pi i$
と,周回積分が $0$ にならないのは円周 $\{\,z\ |\ |z|=r\,\}$ の内部に「穴が開いている」からであって,$z=0$ を避けて,例えば円周 $\{\,z\ |\ |z-2|=1\,\}$ などを考えれば,この円周を含み $z=0$ を含まない単連結領域がとれるから,Cauchyの積分定理が適用できて
$\displaystyle \oint_{|z-2|=1}\dfrac{1}{z}\,dz=0$
となる.
Cauchyの積分定理により,ある領域で正則な関数の複素周回積分はその領域内で積分路を変更できることになる
詳しく!.
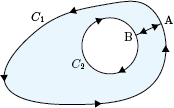
複素関数 $f$ が領域 $D$ で正則であって,$D$ に含まれる閉曲線 $C_1$ に沿った周回積分を考える.
このとき
のように,もう一つの閉曲線 $C_2$ が $C_1$ の内部にあり,$C_1$ と $C_2$ で挟まれた領域(着色部分)が $D$ に含まれているならば,
$\displaystyle \oint_{C_1}f(z)\,dz=\oint_{C_2}f(z)\,dz$
が成り立つ.
なぜなら,矢印のように点 $\mathrm{A}$ から出発し$C_1$上を一周し$\mathrm{A}\rightarrow \mathrm{B}$と中に入って$C_2$上を一周し,再び$\mathrm{B}\rightarrow \mathrm{A}$と点$\mathrm{A}$ に戻ってくる積分路を考えると
($D$ 全体が単連結でないとしても)この閉曲線が囲む部分は単連結であるから,Cauchyの積分定理が適用できて
$\displaystyle \oint_{C_1}f(z)\,dz+\oint_{-C_2}f(z)\,dz=0$
となるからである(直線部分は打ち消し合い,$C_2$ 上は逆回りであることに注意).
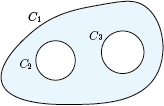
同様に考えると
のような状況では
$\displaystyle \oint_{C_1}f(z)\,dz=\oint_{C_2}f(z)\,dz+\oint_{C_3}f(z)\,dz$
が成り立つことがわかるであろう.
記号の節約のために,円周に沿った周回積分は $\displaystyle \oint_{|z-a|=r}$ のように表記することにしよう.
前項で見た周回積分は,中心をずらして
$\displaystyle \oint_{|z-a|=r}(z-a)^n\,dz
=\left\{\begin{array}{ll}
2\pi i&(n=-1)\\
0&(n\neq -1)
\end{array}\right.
$
としても成り立つことは容易に確認できる.
そこで,
$\displaystyle \oint_{|z|=2}\dfrac{1}{z(z+1)}\,dz$
という積分を考えよう.
$\dfrac{1}{z(z+1)}=\dfrac{1}{z}-\dfrac{1}{z+1}$ であって,
円周 $\{\,z\ |\ |z|=2\,\}$ は被積分関数の特異点(分母が $0$ となる点) $z=0,-1$ を内部に含むから,これらに触らないように積分路を変更して,例えば
$\displaystyle \oint_{|z|=2}\dfrac{1}{z(z+1)}\,dz
=\oint_{|z|=\frac{1}{2}}\dfrac{1}{z}\,dz-\oint_{|z+1|=\frac{1}{2}}\dfrac{1}{z+1}\,dz$
とすることができる.右辺は第一項,第二項ともに $2\pi i$ に等しいから
$\displaystyle \oint_{|z|=2}\dfrac{1}{z(z+1)}\,dz=2\pi i-2\pi i=0$
という結果が得られる.
Cauchyの積分公式
次の
Cauchyの積分公式は,複素周回積分の計算において基本的な役割を果たす:
複素関数 $f$ が単連結領域 $D$ で正則ならば,$D$ に含まれる任意の閉曲線 $C$ および $C$ の内部の点 $a$ について
$\displaystyle \oint_C\dfrac{f(z)}{z-a}dz=2\pi if(a)$
が成り立つ
証明pdf.
表式を見るとあるいは唐突な印象を受けるかもしれないが
$\displaystyle \oint_{|z|=\varepsilon}\dfrac{1}{z}dz=2\pi i$
が $\varepsilon > 0$ をどんなに小さくとっても成り立つことと,
$\varepsilon$ が非常に $0$ に近ければ $f(z)$ は $f(0)$ に非常に近い($f$ の連続性)ことに注意すると,$0$ が閉曲線 $C$ の内部にあるとき
$\displaystyle
\oint_C\dfrac{f(z)}{z}dz=
\oint_{|z|= \varepsilon }\dfrac{f(z)}{z}dz\\[1mm]
\hspace{45pt}\displaystyle \sim f(0)\oint_{|z|= \varepsilon}\dfrac{1}{z}dz= 2\pi if(0)$
となるであろうことは自然に推測できよう.
関数 $\dfrac{\cos{\pi z}}{(z-1)(z-3)}$ の,三つの円周
$\{\,z\ |\ |z| = 1/2\,\}$
$\{\,z\ |\ |z| = 2\,\}$
$\{\,z\ |\ |z| = 4\,\}$
に沿っての周回積分を考える.
$\dfrac{\cos{\pi z}}{(z-1)(z-3)}$ は単連結領域 $\{\,z\ |\ |z| < 1\,\}$ で正則なので,この領域に含まれる円周 $\{\,z\ |\ |z| = 1/2\,\}$ に沿った周回積分は,Cauchyの積分定理により $0$ となる:
$\displaystyle \oint_{|z|=1/2}\dfrac{\cos{\pi z}}{(z-1)(z-3)}dz=0$
$\dfrac{\cos{\pi z}}{z-3}$ は単連結領域 $\{\,z\ |\ |z| < 3\,\}$ で正則,円周 $\{\,z\ |\ |z| = 2\,\}$ は点 $z=1$ を内部に含み, $\{\,z\ |\ |z| < 3\,\}$ に含まれるので,
$\dfrac{\cos{\pi z}}{(z-1)(z-3)}=\dfrac{\cos{\pi z}/(z-3)}{z-1}$ と考えてCauchyの積分公式を適用すると
$\displaystyle \oint_{|z|=2}\dfrac{\cos{\pi z}}{(z-1)(z-3)}dz
=\dfrac{\cos{\pi z}}{z-3}\,\bigg|_{z=1}\\[1mm]
\hspace{98pt}=\dfrac{\cos{\pi}}{-2}=\dfrac{1}{2}$
$z=1$,$z=3$ は 円周 $\{\,z\ |\ |z| = 4\,\}$ の内部に含まれるので,適当に積分路を取り換えることでCauchyの積分公式を適用できる.
$\dfrac{\cos{\pi z}}{(z-1)(z-3)}=\dfrac{\cos{\pi z}/(z-3)}{z-1}=\dfrac{\cos{\pi z}/(z-1)}{z-3}$ と考えて
$\displaystyle \oint_{|z|=4}\dfrac{\cos{\pi z}}{(z-1)(z-3)}dz
=\dfrac{\cos{\pi z}}{z-3}\,\bigg|_{z=1}+\dfrac{\cos{\pi z}}{z-1}\,\bigg|_{z=3}\\[1mm]
\hspace{98pt}=\dfrac{\cos{\pi}}{-2}+\dfrac{\cos{3\pi}}{2}=0$