実定積分の計算
前講の留数定理を利用して，実定積分
$\displaystyle \int_{-\infty}^\infty\dfrac{dx}{x^2+1}$
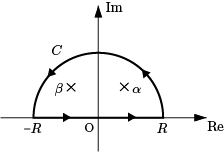
を計算してみよう．積分経路を
のようにとり，複素周回積分 $\displaystyle \oint_C\dfrac{dz}{z^2+1}$ を考える．
$R$ が大きいとき，被積分関数の $C$ の内部に含まれる特異点は $i$ であり，
留数は
$\underset{z=i}{\mathrm{Res}}\dfrac{1}{z^2+1}=\dfrac{1}{1+i}\Big|_{z=i}=\dfrac{1}{2i}$
である．よって留数定理により
$\displaystyle \oint_C\dfrac{dz}{z^2+1}=2\pi i\cdot\dfrac{1}{2i}=\pi$
が成り立ち，円弧上では $z=Re^{i\theta}\ (0\le\theta\le \pi)$ とおけるから，$dz=Rie^{i\theta}d\theta$ に注意して，上式は
$\displaystyle \int_{-R}^R\dfrac{dx}{x^2+1}+\int_0^\pi\dfrac{Rie^{i\theta}d\theta}{R^2e^{2i\theta}+1}=\pi\hspace{40pt}(*)$
となる．
ここで，$R>1$ のとき $|R^2e^{2i\theta}+1|\ge |R^2e^{2i\theta}|-1=R^2-1$ であるから
$\displaystyle
\left|\int_0^\pi\dfrac{Rie^{i\theta}d\theta}{R^2e^{2i\theta}+1}\right|
\le \int_0^\pi\dfrac{|Rie^{i\theta}|}{|R^2e^{2i\theta}+1|}d\theta\\[1mm]
\hspace{69pt}\le \displaystyle\int_0^\pi\dfrac{R}{R^2-1}d\theta\\[1mm]
\hspace{69pt}=\dfrac{R}{R^2-1}\pi
\underset{R\to\infty}{\longrightarrow}0$
よって $(*)$ で $R\to\infty$ として
$\displaystyle \int_{-\infty}^\infty \dfrac{dx}{x^2+1}=\pi$
を得る．
この結果は
$\dfrac{d}{dx}\arctan{x}=\dfrac{1}{x^2+1}$
より
$\displaystyle \int_{-\infty}^\infty \dfrac{dx}{x^2+1}=\arctan{x}\Big|_{-\infty}^\infty=\dfrac{\pi}{2}-\Big(-\dfrac{\pi}{2}\Big)=\pi$
と容易に得られるのであるが，留数定理の実定積分への典型的な応用例として，計算の様子をよく観察しておきたい．
同様の方法で
$\displaystyle \int_{-\infty}^\infty\dfrac{x^2}{x^4+1}dx$
を計算してみよう．積分経路を同じく
とり，複素周回積分 $\displaystyle \oint_C\dfrac{z^2}{z^4+1}dz$ を考える．
$R$ が大きいとき，被積分関数の $C$ の内部に含まれる特異点は $\alpha = e^{\frac{\pi}{4}i}=\dfrac{1+i}{\sqrt{2}}$，$\beta = e^{\frac{3}{4}\pi i}=\dfrac{-1+i}{\sqrt{2}}$ であり，それぞれ留数を調べると
$\displaystyle \underset{z=\alpha}{\mathrm{Res}}\dfrac{z^2}{z^4+1}
=\lim_{z\to\alpha}\dfrac{(z-\alpha)z^2}{z^4+1}\\[1mm]
\hspace{47pt}=\displaystyle \lim_{z\to\alpha}\dfrac{3z^2-2\alpha z}{4z^3}
=\dfrac{1}{4\alpha}=\dfrac{1-i}{4\sqrt{2}}
$
$\displaystyle \underset{z=\beta}{\mathrm{Res}}\dfrac{z^2}{z^4+1}
=\cdots=\dfrac{1}{4\beta}=\dfrac{-1-i}{4\sqrt{2}}
$
とわかる．ここでL'Hospitalの定理を用いた．よって留数定理により
$\displaystyle \oint_C\dfrac{z^2}{z^4+1}dz=2\pi i\Big(\dfrac{1-i}{4\sqrt{2}}+\dfrac{-1-i}{4\sqrt{2}}\Big)=\dfrac{\sqrt{2}}{2}\pi$
が成り立ち，従って
$\displaystyle \int_{-R}^R\dfrac{x^2}{x^4+1}dx+\int_0^\pi\dfrac{R^3ie^{3i\theta}d\theta}{R^4e^{4i\theta}+1}=\dfrac{\sqrt{2}}{2}\pi\hspace{30pt}(**)$
となる．ここで
$\displaystyle
\left|\int_0^\pi\dfrac{R^3ie^{3i\theta}d\theta}{R^4e^{4i\theta}+1}\right|
\le \int_0^\pi\dfrac{|R^3ie^{3i\theta}|}{|R^4e^{4i\theta}+1|}d\theta\\[1mm]
\hspace{69pt}\le \displaystyle \int_0^\pi\dfrac{R^3}{R^4-1}d\theta=\dfrac{R^3}{R^4-1}\pi
\underset{R\to\infty}{\longrightarrow}0$
よって $(**)$ で $R\to\infty$ として
$\displaystyle \int_{-\infty}^\infty \dfrac{x^2}{x^4+1}dx=\dfrac{\sqrt{2}}{2}\pi$
を得る．
複素周回積分を利用した計算のもう一つの典型例は
$\displaystyle \int_0^{2\pi}\dfrac{dx}{5+4\cos{x}}$
のような形の積分である．これは $\cos{x}=\dfrac{e^{ix}+e^{-ix}}{2}$ より
$\displaystyle \int_0^{2\pi}\dfrac{dx}{5+4\cos{x}}
=\int_0^{2\pi}\dfrac{dx}{5+2e^{ix}+2e^{-ix}}\\[1mm]
\hspace{70pt}=\displaystyle \int_0^{2\pi}\dfrac{e^{ix}dx}{2e^{2ix}+5e^{ix}+2}$
と表わせるから，ここで $z=e^{ix}$ とおくと，
$\{\,e^{ix}\ |\ 0\le x\le2\pi\,\}=\{\,z\ |\ |z|=1\,\}$ であり，$dz=ie^{ix}dx$ ゆえ
$\displaystyle \int_0^{2\pi}\dfrac{dx}{5+4\cos{x}}
=\dfrac{1}{i}\oint_{|z|=1}\dfrac{dz}{2z^2+5z+2}\\[1mm]
\hspace{70pt}=\displaystyle \dfrac{1}{i}\oint_{|z|=1}\dfrac{dz}{2(z+2)(z+1/2)}$
となり，最右辺の形の積分はCauchyの積分公式(または留数定理)により計算できる．すなわち，
円周 $|z|=1$ の内部に含まれる特異点は $z=-\dfrac{1}{2}$ だから
$\displaystyle
\oint_{|z|=1}\dfrac{dz}{2(z+2)(z+1/2)}
=2\pi i\cdot\dfrac{1}{2(z+2)}\bigg|_{z=-1/2}\\[1mm]
\hspace{103pt}=\dfrac{2\pi i}{3}$
従って，求める積分の値は
$\displaystyle \int_0^{2\pi}\dfrac{dx}{5+4\cos{x}}=\dfrac{2}{3}\pi$
となる．
同様の方法で
$\displaystyle \int_0^{2\pi}\dfrac{dx}{2-\sin{x}}$
を計算してみよう．$\sin{x}=\dfrac{e^{ix}-e^{-ix}}{2i}$ より
$\displaystyle \int_0^{2\pi}\dfrac{dx}{2-\sin{x}}
=\int_0^{2\pi}\dfrac{2idx}{4i-e^{ix}+e^{-ix}}\\[1mm]
\hspace{62pt}=\displaystyle\int_0^{2\pi}\dfrac{-2ie^{ix}dx}{e^{2ix}-4ie^{ix}-1}$
ここで，$z=e^{ix}$とおくと
$\displaystyle \int_0^{2\pi}\dfrac{dx}{2-\sin{x}}
=\oint_{|z|=1}\dfrac{-2dz}{z^2-4iz-1}$
となる．右辺の被積分関数の特異点を調べると $z=(2\pm\sqrt{3})i$ とわかり，円周 $|z|=1$ の内部に含まれるのは $z=(2-\sqrt{3})i$ のほうであるから，
これもCauchyの積分公式(または留数定理)により
$\displaystyle
\oint_{|z|=1}\dfrac{dz}{z^2-4iz-1}
=2\pi i\cdot\dfrac{1}{z-(2+\sqrt{3})i}\bigg|_{z=(2-\sqrt{3})i}\\[1mm]
\hspace{81pt}=-\dfrac{\pi}{\sqrt{3}}$
従って，求める積分の値は
$\displaystyle \int_0^{2\pi}\dfrac{dx}{2-\sin{x}}=\dfrac{2}{\sqrt{3}}\pi$
となる．
級数の総和法
留数定理はいろいろな級数の計算にも利用できる．
典型的な例として，関数 $\cot{\pi z}$ が整数点に特異点をもつ
詳しく！
$\cot{\pi z}=\dfrac{\cos{\pi z}}{\sin{\pi z}}=\dfrac{e^{\pi iz}+e^{-\pi iz}}{e^{\pi iz}-e^{-\pi iz}}i$ の特異点は $e^{\pi iz}-e^{-\pi iz}=0$ となる点だから，確かに $z=n\ (n\in\mathbf{Z})$ である．
ことを利用して
$\displaystyle \sum_{n=1}^\infty\dfrac{1}{n^2}$
を計算してみよう．
鍵となるのは，$N\in\mathbf{N}$ とし，上図のような
$\alpha=(N+1/2)(1+i)$
$\beta=(N+1/2)(-1+i)$
$\gamma=(N+1/2)(-1-i)$
$\delta=(N+1/2)(1-i)$
を頂点とする正方形 $C_N$ を考えたとき，$N$ に依らない定数 $M > 0$ が存在して
$|\cot{\pi z}|\le M\quad(\forall z\in C_N)$
とできることである
証明．
まず，実軸に平行な線分上で考える．$z=x+yi$とおくと
$|\cot{\pi z}|=\left|\dfrac{\cos{\pi z}}{\sin{\pi z}}\right|\\[1mm]
\hspace{33pt}=\left|\dfrac{e^{\pi iz}+e^{-\pi iz}}{e^{\pi iz}-e^{-\pi iz}}\right|\\[1mm]
\hspace{33pt}=\left|\dfrac{e^{\pi ix-\pi y}+e^{-\pi ix+\pi y}}{e^{\pi ix- \pi y}-e^{-\pi ix+\pi y}}\right|\\[1mm]
\hspace{33pt}\le\dfrac{|e^{\pi ix-\pi y}|+|e^{-\pi ix+\pi y}|}{\big|\,|e^{\pi ix-\pi y}|-|e^{-\pi ix+\pi y}|\,\big|}\\[1mm]
\hspace{33pt}=\dfrac{e^{\pi y}+e^{-\pi y}}{|e^{\pi y}-e^{-\pi y}|}
$
となるから，$\alpha$ と $\beta$ を結ぶ線分上では $y=N+\frac{1}{2}\ge\frac{1}{2}$ より
$|\cot{\pi z}|
\le\dfrac{e^{\pi y}+e^{-\pi y}}{e^{\pi y}-e^{-\pi y}}
=\dfrac{e^{2\pi y}+1}{e^{2\pi y}-1}\\[1mm]
\hspace{33pt}=1+\dfrac{2}{e^{2\pi y}-1}
\le 1+\dfrac{2}{e^{\pi}-1}
$
$\gamma$ と $\delta$ を結ぶ線分上では $y=-N-\frac{1}{2}\le-\frac{1}{2}$ より
$|\cot{\pi z}|
\le\dfrac{e^{-\pi y}+e^{\pi y}}{e^{-\pi y}-e^{\pi y}}
=\dfrac{e^{-2\pi y}+1}{e^{-2\pi y}-1}\\[1mm]
\hspace{33pt}
=1+\dfrac{2}{e^{-2\pi y}-1}
\le 1+\dfrac{2}{e^{\pi}-1}
$
また，虚軸に平行な線分上では $z=\pm (N+\frac{1}{2})+yi$ とおけるから
$|\cot{\pi z}|
=\left|\dfrac{\cos{\pi \{\pm(N+\frac{1}{2})+yi\}}}{\sin{\pi \{\pm(N+\frac{1}{2})+yi\}}}\right|\\[1mm]
\hspace{33pt}
=\left|\dfrac{\sin{\pi yi}}{\cos{\pi yi}}\right|
=\dfrac{|e^{-\pi y}-e^{\pi y}|}{e^{-\pi y}+e^{\pi y}}
\le 1
$
以上より，$C_N$ 上で
$|\cot{\pi z}|\le 1+\dfrac{2}{e^\pi-1}$
が成り立つ．$|\cot{\pi z}|$ が $N$ に依らない定数で抑えられていることに注意しよう．
このことに注意しておいて，$f(z)=\dfrac{\pi\cot{\pi z}}{z^2}$ とおき，
$f(z)$ の特異点 $z=n\ (n\in\mathbf{Z})$ における留数を計算する．
まず，$n\neq0$ のときは $z=n$ は $1$ の極であるから
$\displaystyle \underset{z=n}{\mathrm{Res}}f(z)
=\lim_{z\to n}\dfrac{(z-n)\pi\cos{\pi z}}{z^2\sin{\pi z}}\\[1mm]
\hspace{35pt}=\displaystyle \lim_{z\to 0}\dfrac{z\pi\cos{\pi z}}{(z+n)^2\sin{\pi z}}
=\dfrac{1}{n^2}$
また，$z=0$ は $3$ 位の極であるから，Laurent展開を実行して
$\displaystyle
\cot{\pi z}
=\dfrac{1-\frac{(\pi z)^2}{2!}+\frac{(\pi z)^4}{4!}-\cdots}{\pi z-\frac{(\pi z)^3}{3!}+\frac{(\pi z)^5}{5!}-\cdots}\\[1mm]
\hspace{26pt}=\dfrac{1}{\pi z}-\dfrac{\pi z}{3}-\dfrac{(\pi z)^3}{45}+\cdots$
より
$\displaystyle \underset{z=0}{\mathrm{Res}}f(z)=-\dfrac{\pi^2}{3}$ とわかる．
$3$ 位の極における留数なので
$\displaystyle \underset{z=0}{\mathrm{Res}}f(z)=\lim_{z\to0}\dfrac{1}{2!}\dfrac{d^2}{dz^2}\{z^3f(z)\}$
と計算してもよいが，このように多項式の除法の要領で(必要な項が得られるまで)割り算を実行することもしばしば有効である．
これらより，上図の閉曲線 $C_N$ 上で $f(z)$ の周回積分を行うと，留数定理により
$\displaystyle \oint_{C_N}f(z)dz
=2\pi i\Big(-\dfrac{\pi^2}{3}+\sum_{n=1}^N\dfrac{1}{n^2}+\sum_{n=-N}^{-1}\dfrac{1}{n^2}\Big)\\[1mm]
\hspace{46pt}\displaystyle=2\pi i\Big(-\dfrac{\pi^2}{3}+2\sum_{n=1}^N\dfrac{1}{n^2}\Big)\qquad(*)$
を得る．ここで，左辺の積分については，
$C_N$ 上では $|z|\ge N+\frac{1}{2}$ であることに注意して
$\displaystyle \bigg|\oint_{C_N}f(z)dz\bigg|
\le \oint_{C_N}\dfrac{\pi|\cot{\pi z}|}{|z|^2}|dz|\\[1mm]
\hspace{53pt}\displaystyle \le \oint_{C_N}\dfrac{ \pi M}{(N+\frac{1}{2})^2}|dz|\\[1mm]
\hspace{53pt}= \dfrac{\pi M \cdot4(2N+1)}{(N+\frac{1}{2})^2}$
となるから，$(*)$ で $N\to\infty$ として
$\displaystyle 0=2\pi i\Big(-\dfrac{\pi^2}{3}+2\sum_{n=1}^\infty\dfrac{1}{n^2}\Big)$
すなわち
$\displaystyle \sum_{n=1}^\infty\dfrac{1}{n^2}=\dfrac{\pi^2}{6}$
が得られる．
関数 $\csc{\pi z}=\dfrac{1}{\sin\pi z}$ も整数点に特異点をもつ．
このことを利用して，同じ積分路 $C_N$ を考えることで
$\displaystyle \sum_{n=1}^\infty\dfrac{(-1)^{n-1}}{n^2}$
を計算することができる．
この場合も，$N$ に依らない定数 $M > 0$ が存在して
$|\csc{\pi z}|\le M\quad(\forall z\in C_N)$
とできることは全く同様に確かめられる．
$f(z)=\dfrac{\pi\csc{\pi z}}{z^2}$ とおくと，
$n\neq0$ のときは $z=n$ は $1$ の極であるから
$\displaystyle \underset{z=n}{\mathrm{Res}}f(z)
=\lim_{z\to n}\dfrac{(z-n)\pi}{z^2\sin{\pi z}}\\[1mm]
\hspace{35pt}=\displaystyle \lim_{z\to 0}\dfrac{z\pi}{(z+n)^2(-1)^n\sin{\pi z}}
=\dfrac{(-1)^n}{n^2}$
また，$z=0$ は $3$ 位の極であるから，Laurent展開
$\displaystyle
\csc{\pi z}
=\dfrac{1}{\pi z-\frac{(\pi z)^3}{3!}+\frac{(\pi z)^5}{5!}-\cdots}\\[1mm]
\hspace{26pt}=\dfrac{1}{\pi z}+\dfrac{\pi z}{6}+\dfrac{7}{360}(\pi z)^3+\cdots$
より
$\displaystyle \underset{z=0}{\mathrm{Res}}f(z)=\dfrac{\pi^2}{6}$ とわかる．
これらより，上図の閉曲線 $C_N$ 上で $f(z)$ の周回積分を行うと，留数定理により
$\displaystyle \oint_{C_N}f(z)dz
=2\pi i\Big(\dfrac{\pi^2}{6}+2\sum_{n=1}^N\dfrac{(-1)^n}{n^2}\Big)$
を得る．ここで，左辺の積分は
$N\to\infty$ のとき $0$ に収束することがやはり同様に確かめられるから
$\displaystyle 0=2\pi i\Big(\dfrac{\pi^2}{6}+2\sum_{n=1}^\infty\dfrac{(-1)^n}{n^2}\Big)$
すなわち
$\displaystyle \sum_{n=1}^\infty\dfrac{(-1)^{n-1}}{n^2}=\dfrac{\pi^2}{12}$
が得られる．
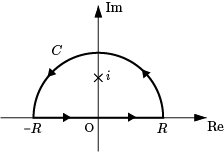のようにとり，複素周回積分 $\displaystyle \oint_C\dfrac{dz}{z^2+1}$ を考える．
$R$ が大きいとき，被積分関数の $C$ の内部に含まれる特異点は $i$ であり，
留数は
複素周回積分を利用した計算のもう一つの典型例は
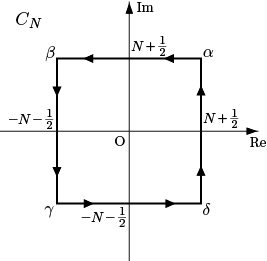鍵となるのは，$N\in\mathbf{N}$ とし，上図のような