第2講 複素関数
複素関数
複素関数は,複素数を複素数に対応させる(すなわち,$\mathbf{C}$ から $\mathbf{C}$ への)写像である.
うるさいことを言うと,「写像」とは,ある集合の一つの要素に対して他の集合の要素を
唯一つ対応させる規則を指す.しかしながら,
例えば,一つの $z$ に無数の実数を対応させる
$f(z)=\arg{z}$
なども歴とした複素関数である(このような関数は
多価関数と呼ばれる).
そういうものも含めて「複素関数」というのであるが,当面はあまり深刻に考える必要はない.
複素関数も実関数と同じく $f(z)$ のように表すことが多いが,$f(z)$ も複素数なので $z=x+yi$ とおいて
$f(x+yi)=u(x,y)+v(x,y)i$
と,二つの $2$ 変数実関数として表すこともできる.
逆にこの形から $f(z)$ の形に戻すには
$\displaystyle x=\dfrac{z+\overline{z}}{2}$,
$\displaystyle y=\dfrac{z-\overline{z}}{2i}$
の関係を用いればよい.
一次関数
$a,b\in\mathbf{C},\ a\neq0$ として,最も基本的な複素関数である一次関数
$f(z)=az+b$
を考えよう.$z$ に $a$ を掛けると$z$ の絶対値は $|a|$ 倍になり,偏角は $\arg{a}$ 増加する
詳しく!.
.
前講で見た複素数の絶対値と偏角に関する性質により
$|az|=|a|\cdot|z|$
$\arg{(az)}=\arg{a}+\arg{z}$
となる.
このことは複素平面上で言えば,ある複素数を掛けることは「拡大(縮小)」および「回転」を意味するということになる.
また,複素数 $b$ を加えることは,複素平面上では実軸方向に $\mathrm{Re}b$,虚軸方向に $\mathrm{Im}{b}$ だけ「平行移動」させることを意味する.
一次関数
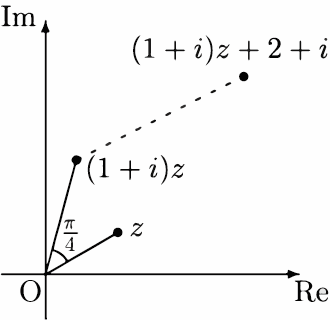
$f(z)=(1+i)z+2+i$
の場合,$1+i=\sqrt{2}\exp\dfrac{\pi}{4}i$,すなわち $|i+i|=\sqrt{2}$,$\arg(1+i)=\dfrac{\pi}{4}$ なので,この関数は複素平面上の各点を「($0$ を中心に) $\pi/4$ 回転させ,($0$ からの距離を) $\sqrt{2}$ 倍に拡大し,さらに $2+i$ だけ平行移動させる」のである.
一次分数変換
$a,b,c,d\in \mathbf{C}$ が $ad-bc\neq0$ を満たすとき,
$f(z)=\dfrac{az+b}{cz+d}$
と表される関数を
一次分数変換,あるいは単に一次変換という.上で見た一次関数も一次分数変換に含まれる.
$ad-bc=0$ だと,約分されて定数関数となってしまうので $ad-bc\neq0$ という条件がついている.
一次分数変換には,円周(または直線)を円周(または直線)に移すという重要な性質がある.
例えば,関数 $f(z)=\dfrac{1}{z}$ が $0$ を中心とする円周をやはり $0$ を中心とする円周に移すことは容易に確かめられる
詳しく!.
実際
$|z|=r \Leftrightarrow \bigg|\dfrac{1}{z}\bigg|=\dfrac{1}{r}$
ゆえ,中心 $0$,半径 $r > 0$ の円周 $\{\,z\ |\ |z|=r\,\}$ は
$f(z)=1/z$ により中心 $0$,半径 $1/r$ の円周に移されることがかわる.
一次分数変換 $f(z)=\dfrac{1}{z-2}$ による.
単位円周 $\{\,z\ |\ |z|=1\,\}$ の像を考えよう.
$w=\dfrac{1}{z-2}$ とおくと $z=\dfrac{1}{w}+2$ ゆえ
$|z|=1\Leftrightarrow\bigg|\dfrac{1}{w}+2\bigg|=1$
となる.
この $w$ についての式は
$\bigg|w+\dfrac{2}{3}\bigg|=\dfrac{1}{3}$
と変形できる
詳しく!
$\bigg|\dfrac{1}{w}+2\bigg|=1$の両辺に $|w|$ を掛けて
$|1+2w|=|w|$
さらに両辺を二乗して展開し整理すると
$3|w|^2+2w+2\overline{w}+1=0$
「平方完成」して
$3\bigg|w+\dfrac{2}{3}\bigg|^2-\dfrac{1}{3}=0$
従って
$\bigg|w+\dfrac{2}{3}\bigg|^2=\dfrac{1}{9}$ が得られる.
から,$f$ は単位円周を中心 $-2/3$,半径 $1/3$ の円周に
移す.
また,中心 $0$,半径 $2$ の場合,すなわち $\{\,z\ |\ |z|=2\,\}$ の像を
同様に考えると
$|z|=1\Leftrightarrow\bigg|\dfrac{1}{w}+2\bigg|=2$
より,右辺を整理して
$w+\overline{w}=-\dfrac{1}{2}$
となる.この式は $\mathrm{Re}w=-\dfrac{1}{4}$ を意味するから,$f$ はこの円周を虚軸に平行な直線に移す.
(注意)
$z=2$ はこの $f$ の定義域から除かなければならないが,敢えて解釈するならば,$f(2)=\infty$,すなわち,$z=2$ は「無限遠点」に移されると言うことができる.このことの正確な意味は後述するが,
一次分数変換は基本的に円周を円周に移すが,円周上に分母を $0$ にするような点があるときは,関数の値はそこで発散して,円が伸びきって直線になってしまう,という捉え方ができるのである.